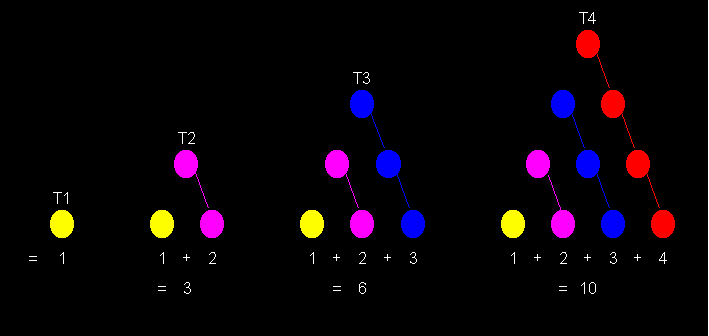
|
Fascinating Triangular Numbers |

The numbers which can be arranged in a compact triangular pattern are termed as triangular numbers. The triangular numbers are formed by partial sum of the series 1+2+3+4+5+6+7......+n. So
T1 = 1
T2 = 1 + 2 = 3
T3 = 1 + 2 + 3 = 6
T4 = 1 + 2 + 3 + 4 = 10
So the nth triangular number can be obtained as Tn = n*(n+1)/2, where n is any natural number.In other words triangular numbers form the series 1,3,6,10,15,21,28.....
Flocks of birds often fly in this triangular formation. Even several airplanes when flying together constitute this formation. The properties of such numbers were first studied by ancient Greek mathematicians, particularly the Pythagoreans.
Have you heard of the following famous story about the famous mathematician Carl F. Gauss.
" The teacher asked everyone in the class to find the sum of all the numbers from 1 to 100. To everybody's surprise, Gauss stood up with the answer 5050 immediately. The teacher asked him as to how it was done. Gauss explained that instead of adding all the numbers from 1 to 100, add first and last term i.e. 1 + 100 =101, then add second and second last term i.e. 2 + 99 =101 and so on. Every pair sum is 101 and their will be 50 such pairs ( total 100 numbers in all to be added), so 101 * 50 = 5050 is the answer. So the sum of numbers from 1 to N is (N/2)*(N+1), where N/2 are the number of pairs and N+1 is sum of each pair. This the famous formula for nth triangular number."
Some of the interesting properties of triangular numbers published in [5] are:
Curious properties of Triangular Numbers:
T1 + T2 = 1 + 3 = 4 = 22
T2 + T3 = 3 + 6 = 9 = 32
9*T1 + 1 = 9 * 1 + 1 = 10 = T4
9*T2 + 1 = 9 * 3 + 1 = 28 = T7
8*T1 + 1 = 8 * 1 + 1 = 9 = 32
8*T2 + 1 = 8 * 3 + 1 = 25 = 52
T42 = 102 = 100 = 13 + 23 + 33 + 43
T52 = 152 = 225 = 13 + 23 + 33 + 43 + 53
T12 + T22 = 1 2 + 3 2= 10 = T4
T22 + T32 = 3 2 + 6 2= 45 = T9
T32 + T42 = 6 2 + 10 2= 136 = T16
Tn-12 + Tn2 = Tn2
(Dr. Diego Marques, University of Brasilia, Brazil submitted vide his email dated 20 Apr 2011 that "this is also valid for the amazing Fibonacci sequence i.e. The sum of the squares
of two consecutive fibonacci numbers is also a fibonacci number).
T12 = 1 * 1 = 1 = T1
T32 = 6 * 6 = 36 = T8
Can anybody find the third triangular number whose square is also a triangular number ?.
(AMRIK S NIMBRAN from Patna, Bihar submitted vide his email dated 21 Dec 2011 that "It took me some time to locate the proof of the impossibility of any other square triangular number
beside 1 and 36 which is square of a triangular number, The source of proof is:
L. J. Mordel, Diophantine Equations, 1969, Academic Press, London, Theorem 7, pp. 268-269).
The largest known palindromic triangular number containing only odd digits:
T32850970 = 539593131395935
The largest known palindromic triangular number containing only even digits:
T128127032 = 8208268228628028
Kn = 34 * Kn-1 - Kn-2 + 2.
So knowing the first two ST numbers i.e. K1 = 1 and K2 = 36 , all other successive Square Triangular numbers can be obtained , e.g.
K3 = 34 * K2 - K1 + 2 = 34 * 36 -1 + 2 = 1225
K4 = 34 * K3 - K2 + 2 = 34 * 1225 - 36 + 2 = 41616
The following non- recursive formula also gives nth Square Triangular number in terms of variable n.
Kn = [{(1 + 2½)2n - (1 - 2½)2n}/(4*2½)]2
It is interesting to note that digital root of all EVEN Square Triangular Numbers i.e. 36, 41616, 48024900, 55420693056 .. etc is always 9 and digital root of all ODD Square Triangular Numbers i.e. 1, 1225, 1413721, 1631432881, ... etc is always 1. Also Square Triangular Numbers can never end in 2, 3, 4, 7, 8 or 9.
21 + 15 = 36 = T8 : 21 - 15 = 6 = T3
171 + 105 = 276 = T23 : 171 - 105 = 66 = T11
703 + 378 = 1081 = T46 : 703 - 378 = 325 = T25
and so on.
T55 = T10 + T54 = T1540 - T1539 = T7 * T10
T75 = T29 + T69 = T77 - T17 = T5 * T19
and so on.
Some New Observations on Triangular Numbers :
1 * 2 * 3 = 6 = T3
4 * 5 * 6 = 120 = T15
5 * 6 * 7 = 210 = T20
9 * 10 * 11 = 990 = T44
56 * 57 * 58 = 185136 = T608
636 * 637 * 638 = 258474216 = T22736
4 * 5 * 6 = 2 * 3 * 4 * 5 = 1 * 2 * 3 * 4 * 5 = 120
No other triangular number is known to be the product of four or more consecutive numbers.
2 * 3 = 6 = T3
14 * 15 = 210 = T20
84 * 85 = 7140 = T119
492 * 493 = 242556 = T696
2870 * 2871 = 8239770 = T4059
16730 * 16731 = 279909630 = T23660
97512 * 97513 = 9508687656 = T137903
568344 * 568345 = 323015470680 = T803760
3312554 * 3312555 = 10973017315470 = T4684659
19306982 * 19306983 = 372759573255306 = T27304196 etc.
2 * 3 = 6 = T3
3 * 5 = 15 = T5
3 * 7 = 21 = T6
5 * 11 = 55 = T10
7 * 13 = 91 = T13
11 * 23 = 253 = T22
19 * 37 = 703 = T37
Harshad (or Niven ) numbers are those numbers which are divisible by their sum of the digits. For example 1729 ( 19*91) is divisible by 1+7+2+9 =19, so 1729 is a Harshad number.
Harshad Triangular Number can be defined as the Triangular numbers which are divisible by the sum of their digits. For example, Triangular number 1128 is divisible by 1+1+2+8 = 12 (i.e. 1128/12 = 94). So 1128 is a Harshad Triangular Number. Other examples are:
1, 3, 6, 10, 21, 36, 45, 120, 153, 171, 190, 210, 300, 351, 378, 465, 630, 666, 780, 820, 990, 1035, 1128, 1275, 1431, 1540, 1596, 1770, 2016, 2080, 2556, 2628, 2850, 2926, 3160, 3240, 3321, 3486, 3570, 4005, 4465, 4560, 4950, 5050, 5460, 5565, 5778, 5886, 7140, 7260, 8001, 8911, 9180, 10011, 10296, 10440, 11175, 11476, 11628, 12720, 13041, 13203, 14196, 14706, 15225, 15400, 15576, 16110, 16290, 16653, 17020, 17205, 17766, 17955, 18145, 18528, 20100, 21321, 21528, 21736, 21945, 22155, 23220, 23436, 24090, 24310, 24976, 25200, 28680, 29646, 30628, 31626, 32640, 33930, 35245, 36585, 37128, 39060, 40470, 41328, 41616, 43365, 43956, 45150, 46360, 51040, 51360, 51681, 52326, 52650, 53956, 56280, 56616, 61776, 63903, 64620, 65341, 67896, 69006, 70125, 70500, 72010, 73536, 73920, 76636, 78210, 79401, 79800, 80200,81810, 88410, 89676, 90100, 93096, 93528, 97020, 100128, 101025, 103740, 105111, 105570 etc.
If you iterate the process of summing the squares of the decimal digits of a number and if the process terminates in 1, then the original number is called a Happy number. For example 7 -> 49 -> 97 -> 130 -> 10 -> 1.
A Happy Triangular Number is defined as a Triangular number which is also a Happy number. For example, consider a triangular number 946, where 946 -> 133 -> 19 -> 82 -> 68 -> 100 -> 1. So 946 is a Happy triangular Number. Other examples of Happy Triangular Numbers are :
1, 10, 28, 91, 190, 496, 820, 946, 1128, 1275, 2080, 2211, 2485, 3321, 4278, 8128, 8256, 8778, 9591, 9730, 11476, 12090, 12880, 13203, 13366, 13530, 15753, 16471, 17205, 17578, 20910, 21115, 21321, 22791, 24753, 25651, 27261, 29890, 30135, 31626, 33670, 35245, 36046, 41328, 43660, 43956, 44253, 46360, 47586, 48205, 50721, 53301, 53956, 54615, 55278, 56280, 56953, 58311, 61425, 62128, 66430, 69378, 69751, 70125, 75855, 76245, 77815, 79003, 80200, 81810, 82621, 84666, 87571, 90100, 90951, 93961, 99681, 100128, 101025, 102831, 103285, 105570, 107416, 110215, 117370, 119316, 122760, 123256, 123753, 126253, 127260, 129286, 130305 etc.
T2 * T24 = 3 * 300 = 900 = 302
T2 * T242 = 3 * 29403 = 88209 = 2972
T3 * T48 = 6 * 1176 = 7056 = 842
T6 * T168 = 21 * 14196 = 298116 = 5462
T11 * T528 = 66 * 139656 = 9217296 = 30362
T12 * T624 = 78 * 195000 = 15210000 = 39002
Note: The product of Ta*Tb is a perfect square for the formula (2a + 1)2 - 1 = b. This produces a perfect square for EVERY triangular index and therefore every triangular number.
(Note submitted by Steve Homewood vide his email dated 27 June 2018).
24 = 16 = T3 + T4 = T1 + T5
34 = 81 = T8 + T9 = T5 + T11
44 = 256 = T15 + T16 = T11 + T19
54 = 625 = T24 + T25 = T19 + T29
64 = 1296 = T35 + T36 = T29 + T41
74 = 2401 = T48 + T49 = T41 + T55
Observe the patterns formed above.
Observation: If n4 = Ta + Tb = Tc + Td then a = n2 - 1, b = n2, c = a - n or n2 - n - 1 and d = a + b - c - 1 or n2 + n - 1.
(Observation submitted by Steve Homewood vide his email dated 1st July 2018).
(reported by Tony Foster vide his email dated 21 January 2024).
T1 + T2 + T3= T4
T5 + T6 + T7 + T8 = T9 + T10
T11 + T12 + T13 + T14 + T15= T16 + T17 + T18
T19 + T20 + T21 + T22 + T23 + T24 = T25 + T26 + T27 + T28
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6
15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
87782 + 102962 = 135302
(T132)2 + (T143)2 = (T164)2
The only known examples of a Pythagorean triangle such that both Perimeter as well as Area are triangular numbers are:
(3312, 14091, 14475) with Perimeter = 31878 = T252 and Area = 23334696 = T6831
(3405996, 8013265, 8707079) with Perimeter = 20126340 = T6344 and Area = 13646574268470 = T5224284
Can you find other examples ? For more visit Carlos Rivera.
John McMahon has discovered the amazing curiosity [15] in the following Pythagorean triplets which are all generated by the Pythagorean triplet (5, 12, 13) by prefixing triangular numbers:
15, 112, 113
25, 312, 313
35, 612, 613
45, 1012, 1013
55, 1512, 1513 and so on.
This can be generalised as follows (where 5 is concatenated with n and, 12, 13 are concatenated with nth triangular numbers):
[n5]2 + [Tn12]2 = [Tn13]2.
(reported by Julian Beauchamp vide his email dated 24 November 2022).
T8 + T35 + T23 = T9 + T21 + T36
8 + 35
+ 23 = 9
+ 21 + 36
T28 + T29 + T30 + ... + T34 = T83
T118 + T119 + T120 + ... + T124 = T321
T16 + T17 + T18 + T19 = 2*T25
T103 + T104 + T105 + T106 = 2*T148
T10 = T5+5 = 55
T100 = T50+50 = 5050
T1000 = T500+500 = 500500
T10000 = T5000+5000 = 50005000
T100000 = T50000+50000 = 5000050000
T1000000 = T500000+500000 = 500000500000 and so on.
TT12 + TT14 = T131
TT15 + TT42 = T911
TT26 + TT34 = T691
TT36 + TT55 = T1678
TT42 + TT120
= T7316 and so on.
13 and 136101521 are primes formed by concatenation of first n triangular numbers. 136 is the only known triangular number formed from concatenation of first n triangular numbers. 31, 631, 10631, 55453628211510631, 786655453628211510631 and 10591786655453628211510631 are primes formed by reverse concatenation of first n triangular numbers [14].
Numbers such that d(n), the number of divisors of n,
is greater than for any smaller n are called highly
composite numbers. If n is a triangular number then it can be termed as Highly Composite Triangular Number . For example 28 is a triangular number and d(28) = 6 . Number of divisors of all triangular numbers less than 28 is less than 6. So 28 is a Highly Composite Triangular number.
All Highly Composite Triangular numbers below 5*1013 are:
1, 3, 6, 28, 36, 120, 300, 528, 630, 2016, 3240, 5460, 25200, 73920, 157080, 437580, 749700, 1385280, 1493856, 2031120, 2162160, 17907120, 76576500, 103672800, 236215980, 842161320, 3090906000, 4819214400, 7589181600, 7966312200, 13674528000, 20366564400, 49172323200, 78091322400, 102774672000, 557736444720, 666365279580, 876785263200, 1787835551040, 2427046221600, 3798207594720, 24287658595200 and 26571463158240.
Numbers such that s(n), the sum of aliquot divisors of n,
is greater than n are called Abundant
numbers. If n is a triangular number then it can be termed as Abundant Triangular Number . For example 36 is a triangular number and s(36) = 1 + 2 + 3 + 4 + 6 + 9 + 12 + 18 = 55, which is greater than 36. So 36 is a Abundant Triangular number.
All Abundant Triangular numbers below 105 are:
36,66,78,120,210,276,300,378,528,630,666,780,820,990,1128,1176,1326,1540,1596, 1770,1830,2016,2080,2346,2556,2628,2850,3160,3240,3486,3570,3828,4095,4278, 4560,4656,4950,5460,5778,5886,6216,6328,6786,7140,7260,7626,7875,8256,8646, 8778,9180,9730,9870,10296,10440,10878,11628,12090,12246,12720,12880,13530, 14028,14196,14706,15400,15576,16110,16290,16836,17020,17766,17955,18336,18528, 19110,19900,20100,20706,20910,21528,21736,21945,22578,23220,23436,24090,24310, 24976,25200,25878,26106,26565,26796,27966,28680,28920,29646,29890,30628,30876, 31626,31878,32640,33670,33930,34716,34980,35778,37128,37950,38226,39060,39340, 40470,41328,41616,42486,43660,43956,44850,45150,46056,46360,47586,48516,48828, 49770,51040,51360,52326,52650,53628,53956,54285,55278,56280,56616,57630,57970, 58996,59340,60378,60726,61425,61776,62128,63546,64620,64980,66066,66430,67896, 69006,69378,70500,72390,73536,73920,75078,76636,77028,78210,78606,79800,80200, 81810,82215,83028,83436,84666,86320,86736,87990,88410,89676,90100,91806,93096, 93528,94830,96580,97020,98346 and 98790.
Numbers such that s(n), the sum of aliquot divisors of n,
is less than n are called Deficient
numbers. If n is a triangular number then it can be termed as Deficient Triangular Number . For example 21 is a triangular number and s(21) = 1 + 3 + 7 = 11, which is less than 21. So 21 is a Deficient Triangular number.
All Deficient Triangular numbers below 105 are:
1,3,10,15,21,45,55,91,105,136,153,171,190,231,253,325,351,406,435,465, 561,595,703,741,861,903,946,1035,1081,1225,1275,1378,1431,1485,1653,1711, 1891,1953,2145,2211,2278,2415,2485,2701,2775,2926,3003,3081,3321,3403,3655, 3741,3916,4005,4186,4371,4465,4753,4851,5050,5151,5253,5356,5565,5671,5995, 6105,6441,6555,6670,6903,7021,7381,7503,7750,8001,8385,8515,8911,9045, 9316,9453,9591,10011,10153,10585,10731,11026,11175,11325,11476,11781,11935, 12403,12561,13041,13203,13366,13695,13861,14365,14535,14878,15051,15225,15753, 15931,16471,16653,17205,17391,17578,18145,18721,18915,19306,19503,19701,20301, 20503,21115,21321,22155,22366,22791,23005,23653,23871,24531,24753,25425,25651, 26335,27028,27261,27495,27730,28203,28441,29161,29403,30135,30381,31125,31375, 32131,32385,32896,33153,33411,34191,34453,35245,35511,36046,36315,36585,36856, 37401,37675,38503,38781,39621,39903,40186,40755,41041,41905,42195,42778,43071, 43365,44253,44551,45451,45753,46665,46971,47278,47895,48205,49141,49455,50086, 50403,50721,51681,52003,52975,53301,54615,54946,55611,55945,56953,57291,58311, 58653,59685,60031,61075,62481,62835,63190,63903,64261,65341,65703,66795,67161, 67528,68265,68635,69751,70125,70876,71253,71631,72010,72771,73153,74305,74691, 75466,75855,76245,77421,77815,79003,79401,80601,81003,81406,82621,83845,84255, 85078,85491,85905,87153,87571,88831,89253,90525,90951,91378,92235,92665,93961, 94395,95266,95703,96141,97461,97903,99235 and 99681.
Take an example of a 10-digit Triangular number 1061444835. It can be seen that this triangular number is the sum of the 10614th and 44835th triangular numbers. So the sum of two triangular numbers is equal to the number formed from concatenation of index of these two triangular numbers.
T10614 + T44835 = 1061444835
Other examples are:
T90 + T415 = 90415
T585 + T910 = 585910
T120 + T1545 = 1201545
T150 + T1726 = 1501726
T244 + T2196 = 2442196
T700 + T3676 = 7003676
T769 + T3846 = 7693846
T1474 + T5226 = 14745226
T2829 + T6970 = 28296970
T3030 + T7171 = 30307171 and so on.
Can you observe beautiful pattern in last two examples.
T6 = 21
T66 = 2211
T666 = 222111
T6666 = 22221111 and so on.
(submitted by William Downie vide his email dated 9 Sept 2015).
T33 = 561
T333 = 55611
T3333 = 5556111 and so on.
The product of any two consecutive numbers in above sequence is a triangular number, which is the product of two consecutive numbers:
√ T1 * √ T8 = 6 = T3 = 2 * 3
√ T8 * √ T49 = 210 = T20 = 14 * 15
√ T49 * √ T288 = 7140 = T119 = 84 * 85
√ T288 * √ T1681 = 242556 = T696 = 492 * 493
√ T1681 * √ T9800 = 8239770 = T4059 = 2870 * 2871
√ T9800 * √ T57121 = 279909630 = T23660 = 16730 * 16731
and so on.(submitted by Dr. N Mander (Mr) from Denmark vide his email dated 22 Oct 2011).
2 * T2 = T3 = 6
2 * T14 = T20 = 210
2 * T84 = T119 = 7140
2 * T492 = T696 = 242556
2 * T2870 = T4059 = 8239770
2 * T16730 = T23660 = 279909630
2 * T97512 = T137903 = 9508687656
2 * T568344 = T803760 = 323015470680
2 * T3312554 = T4684659 = 10973017315470
2 * T19306982 = T27304196 = 372759573255306
and so on.With a0 = 0 and b0 = 0 , the following recursive equations can give further values of a and b:
an=3 * an-1 + 2 * bn-1 + 2
bn=4 * an-1 + 3 * bn-1 + 3
(submitted by Mr Roy Blatchford vide his email dated 17 Mar 2011).
3 * T1 = T2 = 3
3 * T5 = T9 = 45
3 * T20 = T35 = 630
3 * T76 = T132 = 8778
3 * T285 = T494 = 122265
3 * T1065 = T1845 = 1702935
3 * T3976 = T6887 = 23718828
3 * T14840 = T25704 = 330360660
3 * T55385 = T95930 = 4601330415
3 * T206701 = T358017 = 64088265153
and so on.With a0 = 0 and b0 = 0 , the following recursive equations can give further values of a and b:
an = 2 * an-1 + bn-1 + 1
bn = 3 * an-1 + 2 * bn-1 + 2
(submitted by Dr. Muniru A. Asiru from Nigeria vide his email dated 28 Dec 2014).
6 * ( T1 + T2 + T3) + 4 = 43
6 * ( T1 + T2 + T3 + T4) + 5 = 53
6 * ( T1 + T2 + T3 + T4 + T5) + 6 = 63
6 * ( T1 + T2 + T3 + T4 + T5 + T6) + 7 = 73
6 * ( T1 + T2 + T3 + T4 + T5 + ...... + Tn-1) + n = n3
(submitted by Don Davis vide his email dated 20 June 2013).
T22 - T12 = 23
T32 - T22 = 33
T42 - T32 = 43
T52 - T42 = 53
Tn2 - Tn-12 = n3
(submitted by Berke Terzioglu vide his email dated 27 May 2015).
Interesting cube pattern with triangular numbers.

(submitted by Tony Foster vide his email dated 24 July 2015).
Connection Between Golden Ratio and Triangular Numbers.
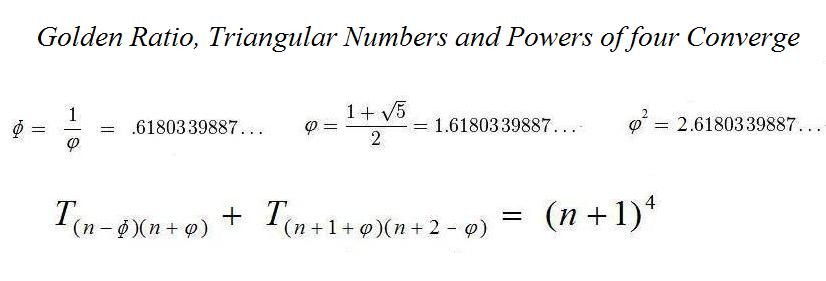
(submitted by Tony Foster vide his email dated 29 July 2015).
Sum of triangular numbers squared in pascals triangle.
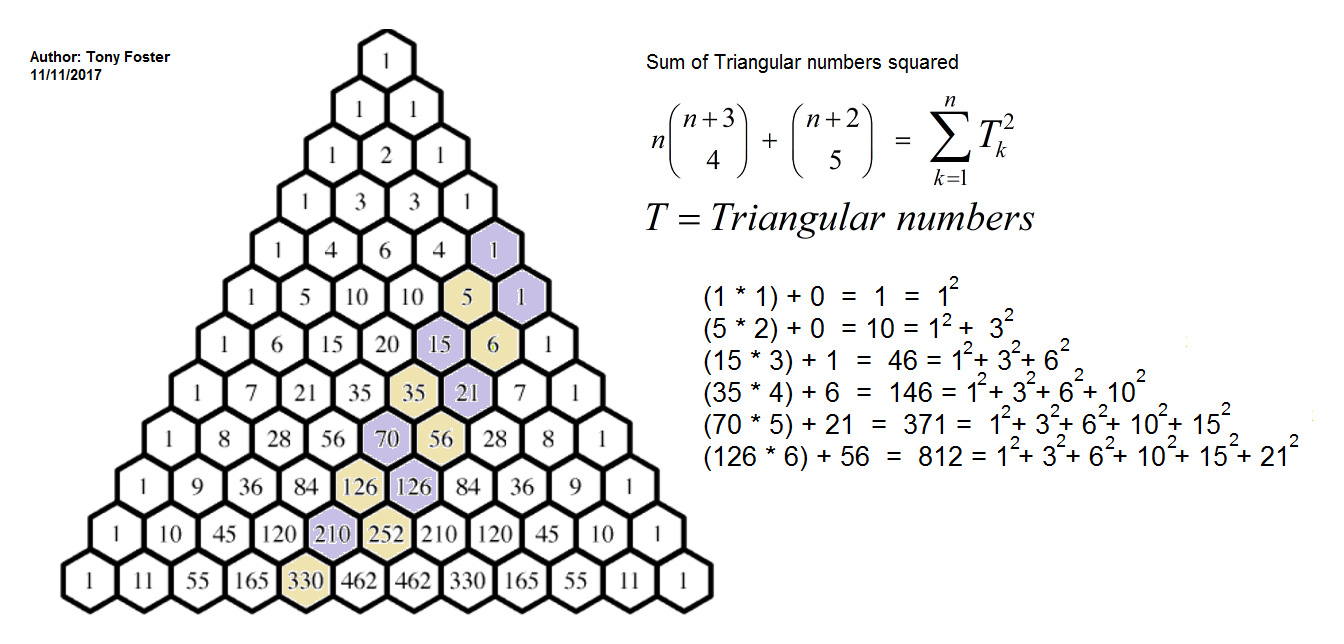
(submitted by Tony Foster vide his email dated 20 November 2017).
A neat triangular number pattern.

(submitted by Tony Foster vide his email dated 17 December 2017).
The sum of reciprocals of squares of all the triangular numbers converges to 4*(π2 - 9)/3:
1 + 1/32 + 1/62 + 1/102 + 1/152 + 1/212 + 1/282 + 1/362 + 1/452 + ....= 4*(π2 - 9)/3
The sum of reciprocals of cubes of all the triangular numbers converges to 8*(10 - π2):
1 + 1/33 + 1/63 + 1/103 + 1/153 + 1/213 + 1/283 + 1/363 + 1/453 + ....= 8*(10 - π2)
(submitted by Okoh Ufuoma Cyrus from Nigeria vide his email dated 26 April 2013).
The sum of reciprocals of squares of triangular numbers with alternating signs is:
1 - 1/32 + 1/62 - 1/102 + 1/152 - 1/212 + 1/282 - 1/362 + 1/452 - ....= 12 - 16*log2 (about 0.9096451110)
The sum of reciprocals of cubes of triangular numbers with alternating signs is:
1 - 1/33 + 1/63 - 1/103 + 1/153 - 1/213 + 1/283 - 1/363 + 1/453 - ....= 96*log2 + 12*zeta(3) - 80 (about 0.9668121717)
(submitted by Mauro Fiorentini vide his email dated 3 January 2015).
T12 + T22 + T32 + T42 + T52+ T62 + T72 = T56
T42 + T52 + T62 + T72 + T82+ T92 + T102 + T112 + T122 = T191
T12 + T22 + T32 + T42 +.......+ T232 + T242 + T252 + T262 = T1196
T12 + T22 + T32 + T42 +.......+ T862 + T872 + T882 + T892 = T24297
T742 + T752 + T762 + T772 +.......+ T1612 + T1622 + T1632 + T1642 = T109577
(submitted by John McMahon vide his email dated 3 May 2018 and 2 December 2018).
Starting with T0 = 0, in base 10,
The sum of the first 10 triangular numbers from T0 to T9 = 165
The sum of the next 10 triangular numbers from T10 to T19 = 1165
The sum of the next 10 triangular numbers from T20 to T29 = 3165
The sum of the next 10 triangular numbers from T30 to T39 = 6165
The sum of the next 10 triangular numbers from T40 to T49 = 10165
The sum of the next 10 triangular numbers from T50 to T59 = 15165
and so on.
The same pattern is evident in other bases. For example, in base 2
Starting with T0 = 0, in base 2,
The sum of the first 2 triangular numbers from T0 to T1 = 1
The sum of the next 2 triangular numbers = 1001
The sum of the next 2 triangular numbers = 11001
The sum of the next 2 triangular numbers = 110001
The sum of the next 2 triangular numbers = 1010001
The sum of the next 2 triangular numbers = 11111001
and so on.
Note that the number of triangular numbers to add must correspond to the base number itself. The last (three?) digits are always the same. The preceding digits are always the triangular numbers (in their respective bases).
(submitted by Julian Beauchamp vide his email dated 9 May 2019).
There is a nice link between triangular numbers and √2 as given below:
as n -> infinity, √Tn+1 - √Tn = √2/2.
The proof is simple:
Using the general formula for triangular numbers, Tn = n(n+1), we get,
√ [(n+1)(n+2)/2] - √[n(n+1)/2] = √2/2.
=> √ [(n+1)(n+2)] - √[n(n+1)] = 1.
But as n tends to infinity, this becomes
√[(n+1)2] - √[n2] = 1
=> (n+1)- n = 1.
Examples: When n is small, as in the case of n = 7, it follows that:
√T8 - √T7 = √36 - √28 = 0.708926927 (= approx √[2]/2 (correct only to 2 decimal places).
But when n = 500, say, the result is correct to 5 decimal places:
√T501 - √T500 = √125751 - √125250 = 0.707107135
This convergence continues as the value of n increases.
(submitted by Julian Beauchamp vide his email dated 17 September 2022).
T233 = T933 + T934 + T935 + ..... + T976 + T977 + T978
(submitted by John McMahon vide his email dated 24 August 2020).
T45 = 1035 and 452 = 2025
T141 = 10011 and 1412 = 19881
T447 = 100128 and 4472 = 199809
T1414 = 1000405 and 14142 = 1999396
T4472 = 10001628 and 44722 = 19998784
T14142 = 100005153 and 141422 = 199996164
T44721 = 1000006281 and 447212 = 1999967841
T141421 = 10000020331 and 1414212 = 19999899241
T447214 = 100000404505 and 4472142 = 200000361796
T1414214 = 1000001326005 and 1414214 2 = 2000001237796
T4472136 = 10000002437316 and 44721362 = 20000000402496
T14142136 = 100000012392316 and 141421362 = 200000010642496
T44721360 = 1000000042485480 and 447213602 = 2000000040249600
T141421356 = 10000000037150046 and 1414213562 = 19999999932878736
and so on.In other bases, the approximated digits for k are of sqrt(2) and sqrt(2*base). In general, the k of p-sided polygonal numbers increasing by one digit approximates the square roots of 2p-4 and, under certain conditions, (2p-4)*base.
(submitted by Mr Tony Sand vide his email dated 11 Mar 2022).
Units Digit of Triangular numbers in base 10:
The units digit of triangular numbers 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, etc.
form a repeating sequence with two halves, where the second half is the mirror image of the first half as shown below:
0, 1, 3, 6, 0, 5, 1, 8, 6, 5, 5, 6, 8, 1, 5, 0, 6, 3, 1, 0, 0, 1, 3, 6, 0, ... (https://oeis.org/A008954 at the Online Encyclopedia of Integer Sequences)
It can be seen that the sequence begins with 0, 1, 3, 6... and ends with ...6, 3, 1, 0.
What explains this mirroring? Consider the second 5 in the sequence, which corresponds to T9 = 45.
45 + 10 = 55
So the next digit in the sequence is 5, mirroring 5. Next consider the second 6 in the sequence, which corresponds to T8 = 36 and so on.
45 + 10 = 55
36 + 9+10+11 = 66
28 + 8+9+10+11+12 = 78
21 + 7+8+9+10+11+12+13 = 91
15 + 6+7+8+9+10+11+12+13+14 = 105
10 + 5+6+7+8+9+10+11+12+13+14+15 = 120
06 + 4+5+6+7+8+9+10+11+12+13+14+15+16 = 136
03 + 3+4+5+6+7+8+9+10+11+12+13+14+15+16+17 = 153
01 + 2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18 = 171
00 + 1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19 = 190
Note how the sum added to each triangular number is always a multiple of 10:
45 + 10 = 45
36 + 9+10+11 = 66 = 36 + (9+11)+10 = 36 + 20+10 = 36 + 30
28 + 8+9+10+11+12 = 78 = 28 + (8+12)+(9+11)+10 = 28 + 20+20+10 = 28 + 50
Adding a multiple of 10 leaves the units digit unaltered. And that's why the first half of the sequence is mirrored in the second half.
The same is true if we consider the units digit of the triangular numbers in base 11.
The units digit of triangular numbers (base 11) 0, 1, 3, 6, A, 14, 1A, 26, 33, 41, 50, 60, 71, 83, 96, AA, 114, 12A, 146, 163, 181, 1A0, 210...
form a repeating sequence which is shorter and is mirrored in a slightly different way as shown below:
0, 1, 3, 6, A, 4, A, 6, 3, 1, 0, 0, 1, 3, 6, A, 4, A, 6, 3, 1, 0, 0
Here's why this happens:
A + 5+6 = 1A (because 5+6 = 10 in base 11)
6 + 4+5+6+7 = 26
3 + 3+4+5+6+7+8 = 33
1 + 2+3+4+5+6+7+8+9 = 41
0 + 1+2+3+4+5+6+7+8+9+A = 50
Note how the sum added to each triangular number is always a multiple of 11:
A + 5+6 = 1A = A + 10
6 + 4+5+6+7 = 26 = 6 + (4+7)+(5+6) = 6 + 10+10 = 6 + 20
3 + 3+4+5+6+7+8 = 33 = 3 + (3+8)+(4+7)+(5+6) = 3 + 10+10+10 = 3 + 30
Adding a multiple of 11 leaves the units digit unaltered in base 11.
Base 10 provides the template for other even bases and base 11 provides the template for other odd bases.
(submitted by Mr Tony Sand vide his email dated 12 May 2023).
Sum of Integers to the fifth Power and Triangular Numbers.

(submitted by Tony Foster vide his email dated 31 August 2022).
Triangular Numbers can be arranged as an infinite sum as follows:
1/101 + 3/102 + 6/103 + 10/104 + 15/105 ...
= 0.1 + 0.03 + 0.006 + 0.0010 + 0.00015 +...
= 0.[137174211248285322359396433470507544581618655692729766803840877914951989026063100]...
(the square brackets indicating a repeating decimal).
= 100/729
Note also how the repeating decimal has the interesting property of being calculable in reverse, working backwards from the last digit, such that:
...00000000000000000001+
...0000000000000000003
...000000000000000006
...00000000000000010
...0000000000000015
...000000000000021
...00000000000028
...0000000000036
...000000000045
….
=.....79149519890260631
(reported by Julian Beauchamp vide his email dated 18 April 2024).
If you find any new and interesting observation about triangular numbers, please email me.
---------------------------------------------------------------------------
[1] Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 59, 1987.
[2] Beiler, Albert H. Recreations in the Theory of Numbers. New York: Dover, 1966.
[3] Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 33-38, 1996.
[4] Dudeney, H. E. Amusements in Mathematics. New York: Dover, pp. 67 and 167, 1970.
[5] Gupta, Shyam Sunder "Curious Properties of triangular numbers." Science Reporter , September 1987, India.
[6] Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 136-138 and 147-150, 1994.
[7] Le Lionnais, F. Les nombres remarquables. Paris: Hermann, 1983.
[8] Madachy, Joseph S. Madachy's Mathematical Recreations. New York: Dover, 1979.
[9] Pickover, Clifford A. Wonders of Numbers. New York: Oxford University Press, 2001.
[10] Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego, CA: Academic Press, 1995.
[11] Trotter, T. Jr. "Some Identities for the Triangular Numbers." J. Recr. Math. 6, 128-135, 1973.
[12] Wells, David. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1997.
[13] Wells, David. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin Books, 1991.
[14] Gupta, Shyam Sunder "Smarandache Sequence of Triangular Numbers", Smarandache Notions Journal, (Vol. 14, 2003).
[15] Dr. Ron Knott Pythagorean Right-Angled Triangles.
This page is created on 26 Oct, 2002.